Normalization

MEOS normalizes sequence or sequence set values that are continuous (that is, when the interpolation is linear or stepwise). For this, consecutive instant values are merged when possible. Recall that two consecutive instant values v1@t1 and v2@t2 define a linear function that states the evolution of the base value between the two timestamps. In this regard, the stepwise interpolation is just a particular case of the linear interpolation when the linear function is constant.

We start by analyzing the case of sequence values. Given three consecutive instant values, the middle value can be deleted if the linear functions defining the evolution of values are the same. This is illustrated in the figure below for linear and stepwise interpolation, where the sequence values in the left are replaced through normalization by the values on the right.

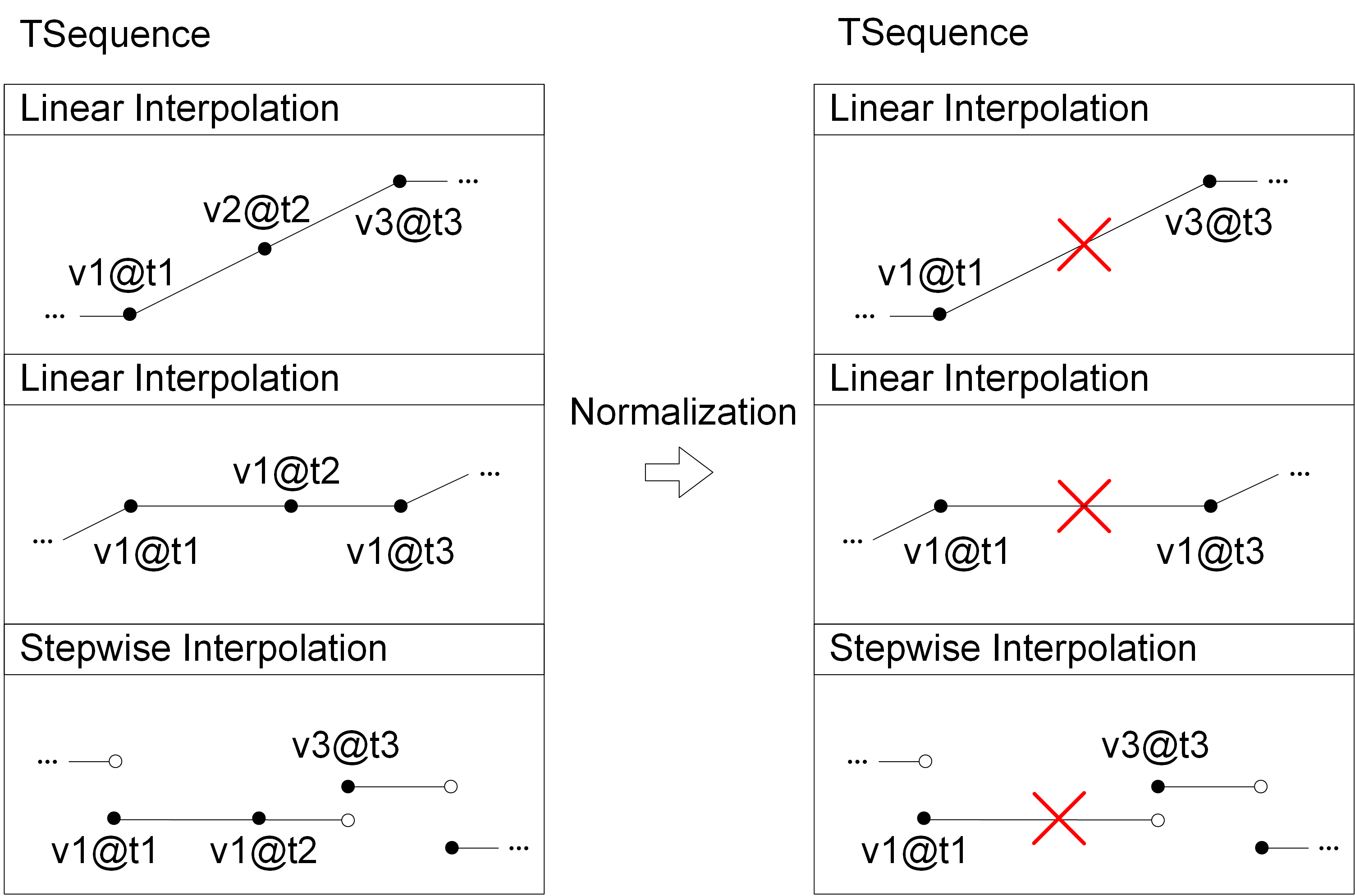
As can be seen, the sequences at the left convey the same information as the sequences at the right. Therefore, normalization ensures that we have a unique representation for equivalent sequences. Examples of normalization for sequence values are shown below

tint '[1@2001-01-01, 2@2001-01-03, 2@2001-01-04, 2@2001-01-05)'
-> [1@2001-01-01, 2@2001-01-03, 2@2001-01-05)
tgeompoint '[Point(1 1)@2001-01-01 08:00:00, Point(1 1)@2001-01-01 08:05:00,
Point(1 1)@2001-01-01 08:10:00)'
-> [Point(1 1)@2001-01-01 08:00:00, Point(1 1)@2001-01-01 08:10:00)
tfloat '[1@2001-01-01, 2@2001-01-03, 3@2001-01-05]'
-> [1@2001-01-01, 3@2001-01-05]
tgeompoint '[Point(1 1)@2001-01-01 08:00:00, Point(2 2)@2001-01-01 08:05:00,
Point(3 3)@2001-01-01 08:10:00]'
-> [Point(1 1)@2001-01-01 08:00:00, Point(3 3)@2001-01-01 08:10:00]

In the case of sequence set values, two composing sequences are merged whenever possible. This is the case when the instant to be removed connects two consecutive sequences. This is illustrated below, where we only consider the case where the first sequence is right exclusive and the second one is left inclusive.

Examples of normalization for sequence set values are shown below

tgeompoint '{[Point(0 0)@2001-01-01 08:00:00,
  Point(1 1)@2001-01-01 08:05:00, Point(1 1)@2001-01-01 08:10:00),
  [Point(1 1)@2001-01-01 08:10:00, Point(1 1)@2001-01-01 08:15:00)}')
-> {[[Point(0 0)@2001-01-01 08:00:00, Point(1 1)@2001-01-01 08:05:00,
  Point(1 1)@2001-01-01 08:15:00)}
tfloat '{[1@2001-01-01, 2@2001-01-03), [2@2001-01-03, 3@2001-01-05]}'
-> '{[1@2001-01-01, 3@2001-01-05]}'
tint '{[1@2001-01-01, 1@2001-01-03), [2@2001-01-03, 2@2001-01-05)}'
-> '{[1@2001-01-01, 2@2001-01-03, 2@2001-01-05)}'
tgeompoint '{[Point(1 1)@2001-01-01 08:00:00,Point(2 2)@2001-01-01 08:05:00),
  [Point(2 2)@2001-01-01 08:05:00, Point(3 3)@2001-01-01 08:10:00]}')
-> {[Point(1 1)@2001-01-01 08:00:00, Point(3 3)@2001-01-01 08:10:00]}
tgeompoint '{[Point(1 1)@2001-01-01 08:00:00,Point(3 3)@2001-01-01 08:10:00),
  [Point(3 3)@2001-01-01 08:10:00]}'
-> {[Point(1 1)@2001-01-01 08:00:00, Point(3 3)@2001-01-01 08:10:00]}

The normalization process is performed by the constructors of the TSequence and TSequenceSet. Therefore, this happens both at the time mobility data is input and when computing the result of any operation. Normalization thus performs lossless compression that can achieve up to 400% compression rate when real-world mobility data is input.